Cameras have a fixed observation field and cannot scan the full FOV of the microscope optics. Consequently, the field must be reduced (by insertion of additional optical components) so that the image can be projected onto the camera sensor without losses.
In scanning microscopes, like true confocal laser scanners, the FN indicates the maximum area over which the sample can be scanned, but the actual scan process must be set with the correct parameters or resolution may be lost. This condition usually means smaller fields should be observed or very large image formats used. To be able to compare these restrictions, a modified field number (RFN) is introduced. RFN refers to the maximum resolved field.
Field number (FN)
The field number (FN) in microscopy is defined as the diameter of the area in the intermediate image plane that can be observed through the eyepiece. A field number of, e.g., 20 mm indicates that the observed sample area after magnification by the objective lens is restricted to a diameter of 20 mm. If the objective lens has a magnification of, say, 40x with an FN of 20 mm, a sample area with a diameter of 500 µm can be observed.
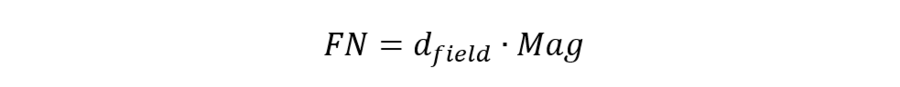
With dfield is the diameter of the observed sample area and Mag is the magnification factor of the objective lens.
Usually, the magnification value is engraved on the lens barrel and the field number is engraved on the eyepiece barrel. With that information, you can always calculate the diameter of the FOV you are currently observing:
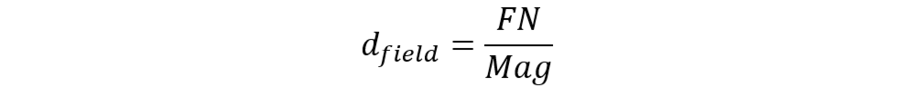
For widefield microscopes, the FN is set by the diameter of a metal diaphragm in the eyepiece. Its size is set to ensure good image quality within the observed field, as all optical systems cause increasing optical aberration far from the center of the lens. Nevertheless, the definition of “good quality” is only standardized for the flatness of field (1), leaving room for discussion about other aberrations.
Confocal scanning
In confocal scanning microscopes, an intermediate image as such is actually not generated. In fact, the pinhole is located in the intermediate image plane. The intensity as a function of time that passes the pinhole, codes for the image information. These intensity changes are subsequently used to reconstruct the image by distribution of the appropriate time-intensity segments into a frame store. The frame store is filled synchronously to the position of the focus spot in the sample. The frame has a predefined size of x times y picture elements (pixels). The tuple (x,y) is called the scan-format or sometimes scan-resolution (not to be confused with the optical resolution (2)).
The calculated FN for a confocal microscope is, therefore, the scanned field size of the sample multiplied by the magnification. The intermediate image does not appear during imaging. By tuning the scanning amplitude, the observed field can be changed from a maximum down to zero (3). Zero amplitude means that a single, fixed spot in the sample is observed, as is required for fluorescence correlation spectroscopy ( FCS ). Intermediate amplitudes generate fields smaller than the maximum, constituting a zoom-in function, because the smaller field is displayed on the same monitor size and, consequently, represents an additional “enlargement” (not an optical magnification).
Optical resolution
The optical resolution (dA) can be determined with the Abbe formula:

where dA is the distance of two infinitesimally small “point” objects that can be just separated, l the wavelength of the illuminating light, and NA the numerical aperture of the objective lens. Obviously, the magnification of the lens has no influence on the optical resolution.
To preserve the optical resolution when scanning a sample and storing the intensities into a digital image, the size of the picture elements projected back from the sample should be smaller than the optical resolution. Otherwise, the digital image has less information than the optical image. As a rule, we assume a factor of ½ times dA as an appropriate oversampling (special image restoring algorithms usually require even higher oversampling, up to fourfold). The required minimal pixel size (dp) can, therefore, be calculated as:

Resolved field
To characterize the power of a confocal scanning microscope, it is not appropriate to discuss the FOV as the full area that is optically corrected, but rather the field that is possible to scan without losses of optical resolution. With the largest possible rectangular scan format (x,y)max, we can calculate the resolved field size (dsc res):

If, for example, we assume λ = 500 nm and NA = 1.4, we have dp = 90 nm. With a scan format of x = y = 1000 pixels, then the field would cover an area of 90 x 90 µm.
If we use a lens that has a magnification of 63x, then the calculated field (equation 1 for FN) would correspond to an area of 5.6 mm x 5.6 mm in the intermediate image plane. The diameter of that square is then only 8 mm and much smaller than typical FNs for which the microscope is designed.
Multiplication of equation 5 by the magnification factor of the lens in use, we get a quantity equivalent to FN, but now taking the actual scanning conditions into account. We call this the resolved field number RFN:

Examples:
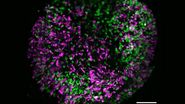
We assume a microscope that is specified with an FN of 22 mm (Fig. 1, left). We use a lens with a magnification of 40x and NA of 1.3, the light wavelength is 500 nm, and we scan a square with x = y = 2496 pixels (considered the maximum the instrument can scan). The RFN then equals 13,6 mm.
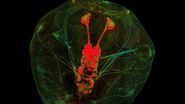
In a second example, we assume a microscope having an FN of 25 mm (Fig 1, right). The same lens (40x/1.3) and light wavelength (500 nm) are used, but the instrument is limited to a maximum of 1024 pixels per dimension. With equation 6, we calculate the RFN to be 5,6 mm. Although for this example, the FN is nominally somewhat larger than in the previous one, the available scan area is much smaller (if we do not accept losses in resolution).